Lombok使用
Lombok 可以通过注解的形式，来帮助我们在开发的时候省略掉一些重复的工作。比如设置 get、set 方法，设置无参构造函数或者全参构造函数。
如果使用的是 IntelliJ IDEA，可以先安装 Lombok Plugin
插件。 最新版已经自带插件可以支持。
然后在项目中引入 jar 文件，如果使用 Maven 构建项目，可以通过在pom.xml中添加以下代码来引用。
Median of Two Sorted Arrays 双数组中位数
题目
4. Median of Two Sorted Arrays
There are two sorted arrays nums1 and nums2 of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
求两个有序数组合并后的中位数。
Letter Combinations of a Phone Number 手机键盘输入组合
题目
17. Letter Combinations of a Phone Number
Given a digit string, return all possible letter combinations that the number could represent. A mapping of digit to letters (just like on the telephone buttons) is given below.
用户按数字键，程序输出所有的可能组合。
What's Next?
题目
What’s Next?
Johnny is playing with a large binary number, B. The number is so large that it needs to be compressed into an array
of integers, A, where the values in even indices (0, 2, 4,...) represent some number of consecutive 1 bits and
the values in odd indices (1, 3, 5,...) represent some number of consecutive 0 bits in alternating substrings of B.
For example, suppose we have array A = {4, 1, 3, 2, 4}. A0 represents "1111", A1
represents "0", A2 represents "111", A3 represents "00", and A4 represents
"1111". The number of consecutive binary characters in ith the substring of B corresponds to integer
Ai, as shown in this diagram:
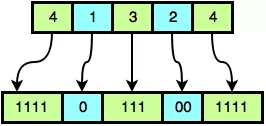
When we assemble the sequential alternating sequences of 1‘s and 0‘s, we get B = 11110111001111.
We define setCount(B) to be the number of 1‘s in a binary number, B. Johnny wants to find a binary number, D,
that is the smallest binary number > B where setCount(B) = setCount(D). He then wants to compress D into an
array of integers, C (in the same way that integer array A contains the compressed form of binary string B).
Johnny isn’t sure how to solve the problem. Given array A, find integer array C and print its length on a new line. Then print the elements of array C as a single line of space-separated integers.