Computers & Technology►Algorithm

What's Next?

题目

What’s Next?

Johnny is playing with a large binary number, B. The number is so large that it needs to be compressed into an array of integers, A, where the values in even indices (0, 2, 4,...) represent some number of consecutive 1 bits and the values in odd indices (1, 3, 5,...) represent some number of consecutive 0 bits in alternating substrings of B.

For example, suppose we have array A = {4, 1, 3, 2, 4}. A0 represents "1111", A1 represents "0", A2 represents "111", A3 represents "00", and A4 represents "1111". The number of consecutive binary characters in ith the substring of B corresponds to integer Ai, as shown in this diagram:

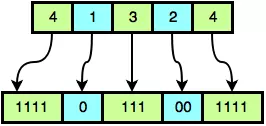
When we assemble the sequential alternating sequences of 1‘s and 0‘s, we get B = 11110111001111.

We define setCount(B) to be the number of 1‘s in a binary number, B. Johnny wants to find a binary number, D, that is the smallest binary number > B where setCount(B) = setCount(D). He then wants to compress D into an array of integers, C (in the same way that integer array A contains the compressed form of binary string B).

Johnny isn’t sure how to solve the problem. Given array A, find integer array C and print its length on a new line. Then print the elements of array C as a single line of space-separated integers.

Input Format

The first line contains a single positive integer, T, denoting the number of test cases. Each of the 2T subsequent lines describes a test case over 2 lines:

  1. The first line contains a single positive integer, , denoting the length of array A.
  2. The second line contains positive space-separated integers describing the respective elements in integer array A (i.e., A0, A1,…, An-1).

Constraints

  • 1 T 100
  • 1 n 10

Subtasks

  • For a score, .
  • For a score, .

Output Format

For each test case, print the following lines:

  1. Print the length of integer array (the array representing the compressed form of binary integer ) on a new line.
  2. Print each element of as a single line of space-separated integers. It is guaranteed that a solution exists.

Sample Input

1
2
3
1
5
4 1 3 2 4

Sample Output

1
2
7
4 1 3 1 1 1 3

Explanation

A = {4, 1, 3, 2, 4}, which expands to B = 11110111001111. We then find setCount(B) = 11. The smallest binary number > B which also has eleven 1‘s is D = 11110111010111. This can be reduced to the integer array C = {4, 1, 3, 1, 1, 1, 3}. This is demonstrated by the following figure:

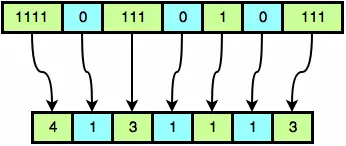
Having found C, we print its length (7) as our first line of output, followed by the space-separated elements in C as our second line of output.

大致意思就是一串二进制数，现在用十进制数来表示几个1和几个0，比如31就是3个1和1个0,11110。现在需要在保持1的个数不变的情况下， 找出大于他的最小的一个数的十进制表示。

思路

用十进制标识有明确的转换说明，不需要考虑，只考虑二进制数的话就是两种情况。

  • 最后跟的全是1：最简单的就是最后全是1，只需要将第一个1和前面的0互换位置就可以，100111 => 101011。

  • 最后跟的全是0：最后全0的时候，需要将前面的全1的第一个1和左边的0呼唤，然后将剩下所有的1和右侧所有的0互换位置。

代码里面分了四种情况，只有一组1的情况单独做了处理，分别是类似于1111、11110000的这两种。因为要用十进制标识，那互换位置之类的就是对应位的数值进行加减。

代码

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
class Solution(object):
    def one(self, nums):
        if nums[0] - 1 == 0:
            return 2, [1, 1]
        else:
            return 3, [1, 1, nums[0] - 1]

    def two(self, nums):
        if nums[0] - 1 == 0:
            return 2, [1, nums[1] + 1]
        else:
            return 3, [1, nums[1] + 1, nums[0] - 1]

    def odd(self, num, nums):
        if nums[-1] - 1 == 0:
            if nums[-2] - 1 == 0:
                del nums[-2]
                nums[-2] += 1
            else:
                nums.insert(-1, 1)
                nums[-3] -= 1
        else:
            nums[-1] -= 1
            nums.insert(-1, 1)
            if nums[-3] - 1 == 0:
                del nums[-3]
                nums[-3] += 1;
            else:
                nums[-3] -= 1
                nums.insert(-2, 1)
        return len(nums), nums

    def even(self, num, nums):
        if nums[-2] - 1 == 0:
            del nums[-2]
            nums[-1] += 1
            if nums[-2] - 1 == 0:
                del nums[-2]
                nums[-2] += 1
            else:
                nums.insert(-1, 1)
                nums[-3] -= 1
        else:
            nums[-1] += 1
            nums.append(nums[-2] - 1)
            del nums[-3]
            if nums[-3] - 1 == 0:
                nums[-4] += 1
                del nums[-3]
            else:
                nums[-3] -= 1
                nums.insert(-2, 1)
        return len(nums), nums

    def solve(self, num, nums):
        if num == 1:
            return self.one(nums)
        if num == 2:
            return self.two(nums)
        if num % 2 == 1:
            return self.odd(num, nums)
        else:
            return self.even(num, nums)



if __name__ == '__main__':
    solution = Solution()
    total = int(input(""))
    result1 = 0
    result2 = []
    for index in range(total):
        num = int(input(""))
        numsString = input("")
        nums = list(map(int, str.split(numsString)))
        result1,result2 = solution.solve(num, nums)
        print(result1)
        print(" ".join(str(x) for x in result2))
分享